Solved The System Has Exactly One Solution Solution The System Has

Solved Best Description Of Its Solution If The System Has Exactly One Step 4: solve the system: use methods such as substitution, elimination, or matrix operations (like gaussian elimination) to find the solution. verify that the solution is unique. solving systems with exactly one solution various methods for solving system of linear equation includes:. A system of two linear equations in two variables has one solution when the two lines have different slopes. from an algebra standpoint, this means that we get a single value when solving the system. visually, the lines intersect exactly once on a graph, since they have different slopes.

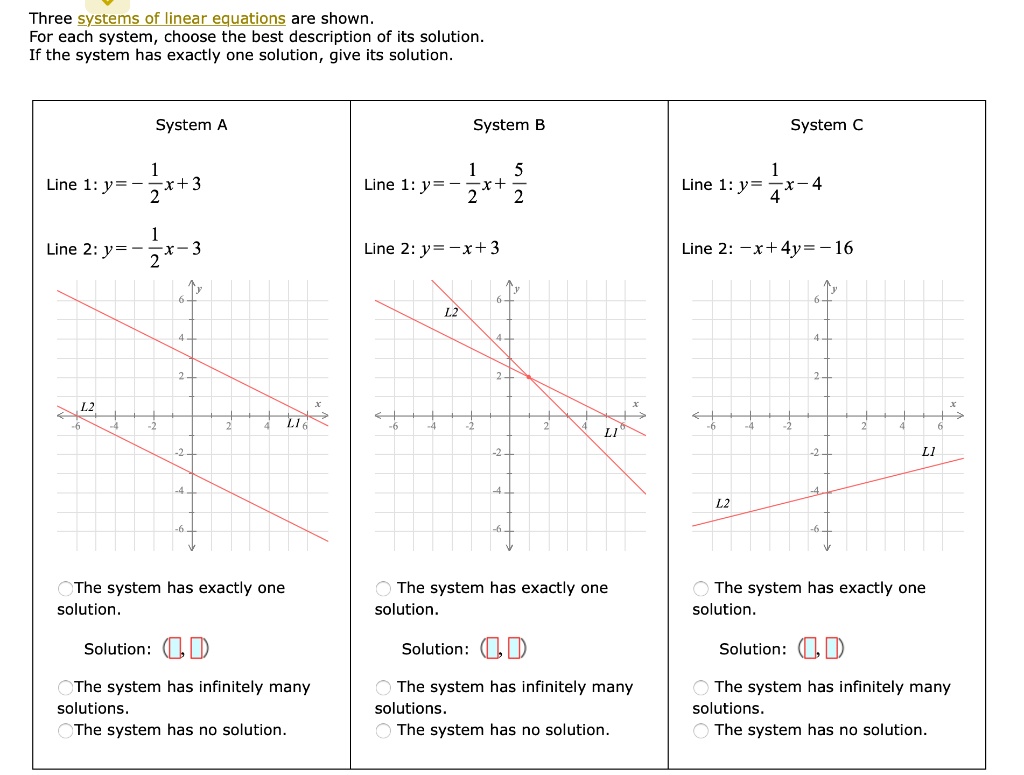
Solved Three Systems Of Linear Equations Are Shown For Each System Thus, the solution to the system is: , this means the system of equations has exactly one solution, which is the point (0, 4.5). an example of a similar problem would be solving the equations 2x 3y = 6 and 4x 6y = 12. you would find that they represent the same line, leading to an infinite number of solutions. In addition to considering the number of equations and variables, we can categorize systems of linear equations by the number of solutions. a consistent system of equations has at least one solution. a consistent system is considered to be an independent system if it has a single solution, such as the example we just explored. A consistent linear system of equations will have exactly one solution if and only if there is a leading 1 for each variable in the system. if a consistent linear system of equations has a free variable, it has infinite solutions. If the given system has exactly one distinct real solution, it follows that 0 = x 2 8 x a 1 5 has exactly one distinct real solution. a quadratic equation in the form 0 = p x 2 q x r, where p, q, and r are constants, has exactly one distinct real solution if and only if the discriminant, q 2 4 p r, is equal to 0.

Solved The System Has Exactly One Solution S Solution The System A consistent linear system of equations will have exactly one solution if and only if there is a leading 1 for each variable in the system. if a consistent linear system of equations has a free variable, it has infinite solutions. If the given system has exactly one distinct real solution, it follows that 0 = x 2 8 x a 1 5 has exactly one distinct real solution. a quadratic equation in the form 0 = p x 2 q x r, where p, q, and r are constants, has exactly one distinct real solution if and only if the discriminant, q 2 4 p r, is equal to 0. 3.4 existence and uniqueness of solutions so far, whenever we have solved a system of linear equations, we have always found exactly one solution. this is not always the case; we will find in this section that some systems do not have a solution, and others have more than one. we start with a very simple example. consider the following linear. One solution: when a system of equations intersects at an ordered pair, the system has one solution. infinite solutions: sometimes the two equations will graph as the same line, in which case we have an infinite number of solutions. The point (x, y, z) = (1, 1, 1) solves the system. the system contains three equations and three variables. during the elimination process, we obtain a false statement. during the elimination process, we obtain the equation 0 = 0. solve the system and determine whether it has exactly one solution or infinitely many solutions. Question 1: the system has exactly one solution. in the first graph, lines l1 and l2 intersect at a single point. by observing the graph, the intersection point is at approximately (0, 1) the system has infinitely many solutions. since the lines intersect at only one point, the system does not have infinitely many solutions. the system has no solution. since the lines intersect at one point.

Solved The System Has Exactly One Solution Solution The System Has 3.4 existence and uniqueness of solutions so far, whenever we have solved a system of linear equations, we have always found exactly one solution. this is not always the case; we will find in this section that some systems do not have a solution, and others have more than one. we start with a very simple example. consider the following linear. One solution: when a system of equations intersects at an ordered pair, the system has one solution. infinite solutions: sometimes the two equations will graph as the same line, in which case we have an infinite number of solutions. The point (x, y, z) = (1, 1, 1) solves the system. the system contains three equations and three variables. during the elimination process, we obtain a false statement. during the elimination process, we obtain the equation 0 = 0. solve the system and determine whether it has exactly one solution or infinitely many solutions. Question 1: the system has exactly one solution. in the first graph, lines l1 and l2 intersect at a single point. by observing the graph, the intersection point is at approximately (0, 1) the system has infinitely many solutions. since the lines intersect at only one point, the system does not have infinitely many solutions. the system has no solution. since the lines intersect at one point.

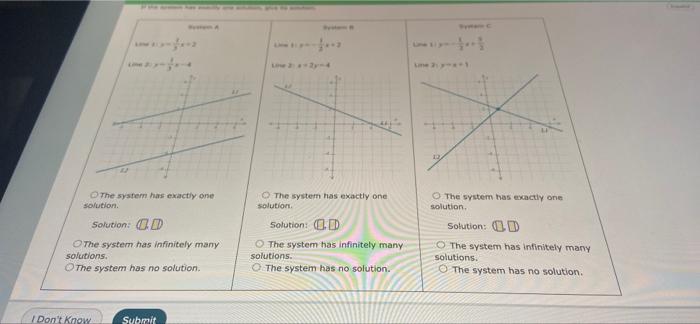
Solved 12 The System Has Exactly One Solution Solution Od Chegg The point (x, y, z) = (1, 1, 1) solves the system. the system contains three equations and three variables. during the elimination process, we obtain a false statement. during the elimination process, we obtain the equation 0 = 0. solve the system and determine whether it has exactly one solution or infinitely many solutions. Question 1: the system has exactly one solution. in the first graph, lines l1 and l2 intersect at a single point. by observing the graph, the intersection point is at approximately (0, 1) the system has infinitely many solutions. since the lines intersect at only one point, the system does not have infinitely many solutions. the system has no solution. since the lines intersect at one point.