Zero One Or Infinitely Many Solutions Passing Linear Algebra
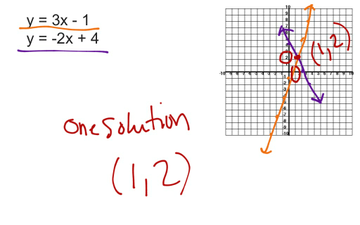
Zero One Or Infinitely Many Solutions Educreations Solution to example problem: 3:38 you only have to row reduce the augmented matrix to row echelon form to determine the number of solutions using the methods. 2. the pair of values you chose is a solution to the first equation. check if it is also a solution to the second equation. then, pause for a brief discussion with your group. compare your answer: your answer may vary, but here is a sample. yes, it is also a solution to the second equation.
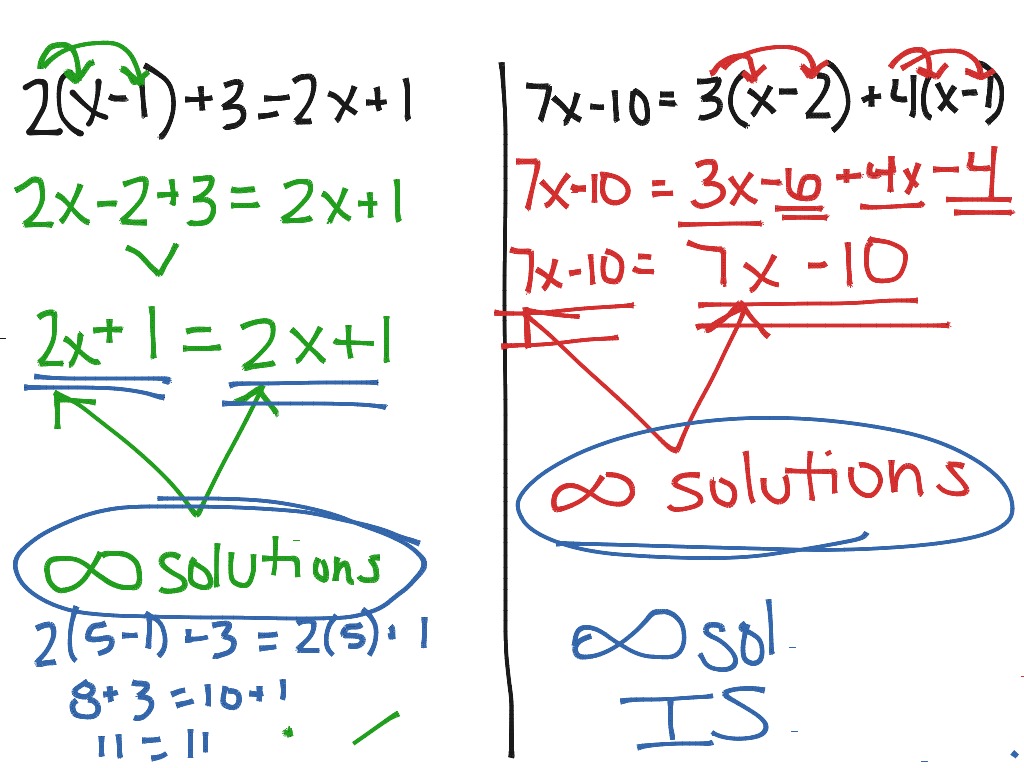
Solving Equations With Zero One Or Infinitely Many 59 Off In this lesson, we will categorize the solutions of a system of two linear equations using the slope intercept form of a line and a plethora of illustrations. 5.3. number of solutions given a system of linear equations, how many solutions are there? we shall see that a system of linear equations has either zero, one, or an infinite number of solutions. This article will explore the concept of "infinitely many solutions" in the context of matrices and linear systems. we'll delve into the conditions that lead to this outcome and provide an "infinitely many solutions matrix example" to illustrate the process. Systems with zero or one solutions may be written by listing their elements, while systems with infinitely many solutions may be written using set builder notation.

Linear Equation With One Infinitely Many No Solution Study Guide This article will explore the concept of "infinitely many solutions" in the context of matrices and linear systems. we'll delve into the conditions that lead to this outcome and provide an "infinitely many solutions matrix example" to illustrate the process. Systems with zero or one solutions may be written by listing their elements, while systems with infinitely many solutions may be written using set builder notation. Since 0x is always 0 regardless of x, any value of x satisfies this equation. so, be careful with problems that reduce to a linear equation. beware that they may have no solutions or an infinite number of solutions. this lesson has been accessed 70301 times. The linear equations with one, zero, or infinite solutions exercise appears under the 8th grade (u.s.) math mission, algebra i math mission and mathematics ii math mission. this exercise helps to understand the difference between equations with one solution, no solutions and many solutions. There could be zero, one, or infinitely many solutions. for example, \displaystyle \left (0,0,0\right) (0, 0, 0) is not a solution to the system below, but that does not mean that it has no solution. Learning objectives: 1) apply elementary row operations to reduce matrices to the ideal form2) classify the solutions as 0, 1, or infinitely many 3) in the i.

Linear Equation With One Infinitely Many No Solution Study Guide Since 0x is always 0 regardless of x, any value of x satisfies this equation. so, be careful with problems that reduce to a linear equation. beware that they may have no solutions or an infinite number of solutions. this lesson has been accessed 70301 times. The linear equations with one, zero, or infinite solutions exercise appears under the 8th grade (u.s.) math mission, algebra i math mission and mathematics ii math mission. this exercise helps to understand the difference between equations with one solution, no solutions and many solutions. There could be zero, one, or infinitely many solutions. for example, \displaystyle \left (0,0,0\right) (0, 0, 0) is not a solution to the system below, but that does not mean that it has no solution. Learning objectives: 1) apply elementary row operations to reduce matrices to the ideal form2) classify the solutions as 0, 1, or infinitely many 3) in the i.

Linear Equation With One Infinitely Many No Solution Study Guide There could be zero, one, or infinitely many solutions. for example, \displaystyle \left (0,0,0\right) (0, 0, 0) is not a solution to the system below, but that does not mean that it has no solution. Learning objectives: 1) apply elementary row operations to reduce matrices to the ideal form2) classify the solutions as 0, 1, or infinitely many 3) in the i.
Comments are closed.